Критерий согласия колмогорова-смирнова - способ оценки распределения совокупности. SPSS в психологии и социальных науках Критерий колмогорова принадлежности генеральной выборке
Назначение критерия . Критерий λ предназначен для сопоставления двух распределений: а). эмпирического с теоретическим, например, равномерным или нормальным; б). одного эмпирического распределения с другим эмпирическим распределением.
Ограничения критерия. Критерий требует, чтобы выборка была достаточно большой, ≥50.
Гипотезы:
: различия между двумя распределениями незначимы.
: различия между двумя распределениями значимы.
Алгоритм подсчета λ – критерия.
Составляем таблицу для удобства расчетов:
1. В первом столбце располагают эмпирические значения признака, упорядоченные по возрастанию.
2. Во втором столбце располагают эмпирические частоты для каждого значения, а в третьем столбце относительные эмпирические частоты для каждого значения, рассчитанные по формуле: f* эмп j = f эмп j / n, где f эмп j – эмпирическая частота из второго столбца, n – объем выборки.
3. Подсчитываем «накопленные» эмпирические частоты по формуле:
∑ f* эмп j = ∑ f* эмп j -1 + f* эмп j ,
где ∑ f* эмп j -1 – частота, накопленная на предыдущих значениях признака;
j – порядковый номер значения признака; f* эмп j – эмпирическая частота данного j разряда. Результаты помещают в 4 столбец.
4. В 5 столбце располагают накопленные теоретические частоты, если сравнивают с известным теоретическим распределением; если сравнивают 2 эмпирических распределения, то в 5 столбце располагают накопленные эмпирические частоты для выборки 2.
5. Подсчитывают разности между накопленными частотами и их абсолютные значения помещают в 6 столбец. Обозначим их d j .
6. Определяют по 6 столбцу максимальное значение d j → d max .
7. Подсчитывают λ эмп по формуле:
,
где n 1 – объем выборки 1, n 2 - объем выборки 2, если = = n, то 
.
8. По заданному уровню значимости из таблицы VII приложения находят граничную точку λ кр.
9. Если λ эмп < λ кр, то различия между распределениями признака незначимы; если λ эмп > λ кр, то различия между распределениями признака значимы.
Пример . В продовольственном магазине проведены контрольные взвешивания проданной колбасы. Объем выборки n = 100. Полученные данные указаны в таблице.
| недовес, г | |||||||||
| частота |
Определить с помощью λ – критерия Колмогорова-Смирнова на уровне значимости α=0,05, согласуются ли данные выборки с равномерным распределением на отрезке .
Решение. : различия между эмпирическим и предполагаемым теоретическим распределением незначимы.
: различия между эмпирическим и предполагаемым теоретическим распределением значимы.
Функция распределения случайной величины, равномерно распределенной на отрезке имеет следующий вид:
Заполним таблицу:
| x j | f эмп j | f эмп j /n | ∑ f* эмп j | ∑ f* теор j | d j |
| 0,10 | 0,10 | 0,1 | |||
| 0,11 | 0,21 | 0,2 | 0,01 | ||
| 0,08 | 0,29 | 0,3 | 0,01 | ||
| 0,09 | 0,38 | 0,4 | 0,02 | ||
| 0,12 | 0,50 | 0,5 | |||
| 0,10 | 0,60 | 0,6 | |||
| 0,13 | 0,73 | 0,7 | 0,03 | ||
| 0,15 | 0,88 | 0,8 | 0,08 | ||
| 0,12 | 1,00 | 0,9 | 0,1 |
Поясним, как заполняется таблица. Значения первых двух столбцов взяты из условия. Каждое число второго столбца делим на n = 100 и результат записываем в 3 столбец. Каждое число 4 столбца равно сумме числа из этой же строки 3 столбца и предыдущего числа 4 столбца. Каждое число 1 столбца подставляем в формулу f * теор = x j /10 и результат записываем в 5 столбец. 6 столбец – модуль разности 4 и 5 столбцов. Наибольшее число в 6 столбце d max =0,1; λ эмп =0,1 = 1.
По уровню значимости α = 0,05 из таблицы VI приложениия находим граничную точку λ кр = 1,358. Поскольку λ эмп < λ кр (1 < 1,358), то принимаем гипотезу на уровне значимости α = 0,05. Данные выборки согласуются с равномерным распределением на отрезке .
Ранее рассматривались гипотезы, в которых закон распределения генеральной совокупности предполагался известным. Теперь займемся проверкой гипотез о предполагаемом законе неизвестного распределения, то есть будем проверять нулевую гипотезу о том, что генеральная совокупность распределена по некоторому известному закону. Обычно статистические критерии для проверки таких гипотез называются критериями согласия.
Критерием согласия называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Это численная мера расхождения между эмпирическим и теоретическим распределением.
Основная задача. Дано эмпирическое распределение (выборка). Сделать предположение (выдвинуть гипотезу) о виде теоретического распределения и проверить выдвинутую гипотезу на заданном уровне значимости α.
Решение основной задачи состоит из двух частей:
1. Выдвижение гипотезы.
2. Проверка гипотезы на заданном уровне значимости.
Рассмотрим подробно эти части.
1. Выбор гипотезы о виде теоретического распределения удобно делать с помощью полигонов или гистограмм частот. Сравнивают эмпирический полигон (или гистограмму) с известными законами распределения и выбирают наиболее подходящий.
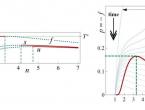
Приведём графики важнейших законов распределения:
Примеры эмпирических законов распределения приведены на рисунках:
 |
|||||||||
 |
|||||||||
В случае (а) выдвигается гипотеза о нормальном распределении, в случае (б) - гипотеза о равномерном распределении, в случае (в) - гипотеза о распределении Пуассона.
Основанием для выдвижения гипотезы о теоретическом распределении могут быть теоретические предпосылки о характере изменения признака. Например, выполнение условий теоремы Ляпунова позволяет сделать гипотезу о нормальном распределении. Равенство средней и дисперсии наводит на гипотезу о распределении Пуассона.
На практике чаще всего приходится встречаться с нормальным распределением, поэтому в наших задачах требуется проверить только гипотезу о нормальном распределении.
Проверка гипотезы о теоретическом распределении отвечает на вопрос: можно ли считать расхождение между предполагаемыми теоретическим и эмпирическим распределениями случайным, несущественным, объясняемым случайностью попадания в выборку тех или иных объектов, или же это расхождение говорит о существенном расхождении между распределениями. Для проверки существуют различные методы (критерии согласия) - c 2 (хи-квадрат), Колмогорова, Романовского и др.
Критерий Пирсона.
Достоинством критерия Пирсона является его универсальность: с его помощью можно проверять гипотезы о различных законах распределения.
1. Проверка гипотезы о нормальном распределении. Пусть получена выборка достаточно большого объема п с большим количеством различных значений вариант. Для удобства ее обработки разделим интервал от наименьшего до наибольшего из значений вариант на s равных частей и будем считать, что значения вариант, попавших в каждый интервал, приближенно равны числу, задающему середину интервала. Подсчитав число вариант, попавших в каждый интервал, составим так называемую сгруппированную выборку:
варианты………..х 1 х 2 … х s
частоты………….п 1 п 2 … п s ,
где х i – значения середин интервалов, а п i – число вариант, попавших в i -й интервал (эмпирические частоты). По полученным данным можно вычислить выборочное среднее и выборочное среднее квадратическое отклонение σ В . Проверим предположение, что генеральная совокупность распределена по нормальному закону с параметрами M (X ) = , D (X ) = . Тогда можно найти количество чисел из выборки объема п , которое должно оказаться в каждом интервале при этом предположении (то есть теоретические частоты). Для этого по таблице значений функции Лапласа найдем вероятность попадания в i -й интервал:
,
где а i и b i - границы i -го интервала. Умножив полученные вероятности на объем выборки п, найдем теоретические частоты: п i =n·p i .Наша цель – сравнить эмпирические и теоретические частоты, которые, конечно, отличаются друг от друга, и выяснить, являются ли эти различия несущественными, не опровергающими гипотезу о нормальном распределении исследуемой случайной величины, или они настолько велики, что противоречат этой гипотезе. Для этого используется критерий в виде случайной величины
. (7)
Смысл ее очевиден: суммируются части, которые квадраты отклонений эмпирических частот от теоретических составляют от соответствующих теоретических частот. Можно доказать, что вне зависимости от реального закона распределения генеральной совокупности закон распределения случайной величины (7) при стремится к закону распределения с числом степеней свободы k = s – 1 – r , где r – число параметров предполагаемого распределения, оцененных по данным выборки. Нормальное распределение характеризуется двумя параметрами, поэтому k = s – 3. Для выбранного критерия строится правосторонняя критическая область, определяемая условием
(8)
где α
– уровень значимости. Следовательно, критическая область задается неравенством 
а область принятия гипотезы - 
.
Итак, для проверки нулевой гипотезы Н 0: генеральная совокупность распределена нормально – нужно вычислить по выборке наблюдаемое значение критерия:
, (7`)
а по таблице критических точек распределения χ 2 найти критическую точку , используя известные значения α и k = s – 3. Если - нулевую гипотезу принимают, при ее отвергают.
Пример. Результаты исследования спроса на товар представлены в таблице:
Выдвинуть гипотезу о виде распределения и проверить её на уровне значимости a=0,01.
I. Выдвижение гипотезы.
Для указания вида эмпирического распределения построим гистограмму
 |
120 160 180 200 220 280
По виду гистограммы можно сделать предположение о нормальном законе распределения изучаемого признака в генеральной совокупности.
II. Проверим выдвинутую гипотезу о нормальном распределении, используя критерий согласия Пирсона.
1. Вычисляем , s В.В качестве вариант возьмём среднее арифметическое концов интервалов:
2. Найдём интервалы (Z i ; Z i+1): 
; 
.
За левый конец первого интервала примем (-¥), а за правый конец последнего интервала - (+¥). Результаты представлены в табл. 4.
3. Найдем теоретические вероятности Р i и теоретические частоты (см. табл. 4).
Таблица 4
| i | Граница интервалов | Ф(Z i) | Ф(Z i+1) | P i = Ф(Z i+1)-Ф(Z i) |  |
|||
| x i | x i+1 | Z i | Z i+1 | |||||
| -¥ | -1,14 | -0,5 | -0,3729 | 0,1271 | 6,36 | |||
| -1,14 | -0,52 | -0,3729 | -0,1985 | 0,1744 | 8,72 | |||
| -0,52 | 0,11 | -0,1985 | 0,0438 | 0,2423 | 12,12 | |||
| 0,11 | 0,73 | 0,0438 | 0,2673 | 0,2235 | 11,18 | |||
| 0,73 | +¥ | 0,2673 | 0,5 | 0,2327 | 11,64 |
4. Сравним эмпирические и теоретические частоты. Для этого:
а) вычислим наблюдаемое значение критерия Пирсона.
Вычисления представлены в табл.5.
Таблица 5
| i | |||||
| 6,36 | -1,36 | 1,8496 | 0,291 | ||
| 8,72 | 1,28 | 1,6384 | 0,188 | ||
| 12,12 | 1,88 | 3,5344 | 0,292 | ||
| 11,18 | 0,82 | 0,6724 | 0,060 | ||
| 11,64 | -2,64 | 6,9696 | 0,599 | ||
| S |
б) по таблице критических точек распределения c 2 при заданном уровне значимости a=0,01 и числе степеней свободы k=m–3=5–3=2 находим критическую точку ; имеем 
.
Сравниваем c . 
.
Следовательно, нет оснований отвергать гипотезу о нормальном законе распределения изучаемого признака генеральной совокупности. Т.е. расхождение между эмпирическими и теоретическими частотами незначимо (случайно). ◄
Замечание. Интервалы, содержащие малочисленные эмпирические частоты (n i <5), следует объединить, а частоты этих интервалов сложить. Если производилось объединение интервалов, то при определении числа степеней свободы по формуле K=m-3 следует в качестве m принять число оставшихся после объединения интервалов.
2. Проверка гипотезы о равномерном распределении . При использовании критерия Пирсона для проверки гипотезы о равномерном распределении генеральной совокупности с предполагаемой плотностью вероятности
необходимо, вычислив по имеющейся выборке значение , оценить параметры а и b по формулам:
где а*
и b*
- оценки а
и b
. Действительно, для равномерного распределения М
(Х
) = , 
, откуда можно получить систему для определения а*
и b
*: 
, решением которой являются выражения (9).
Затем, предполагая, что 
, можно найти теоретические частоты по формулам
Здесь s – число интервалов, на которые разбита выборка.
Наблюдаемое значение критерия Пирсона вычисляется по формуле (7`), а критическое – по таблице с учетом того, что число степеней свободы k = s – 3. После этого границы критической области определяются так же, как и для проверки гипотезы о нормальном распределении.
3. Проверка гипотезы о показательном распределении. В этом случае, разбив имеющуюся выборку на равные по длине интервалы, рассмотрим последовательность вариант , равноотстоящих друг от друга (считаем, что все варианты, попавшие в i – й интервал, принимают значение, совпадающее с его серединой), и соответствующих им частот n i (число вариант выборки, попавших в i – й интервал). Вычислим по этим данным и примем в качестве оценки параметра λ величину . Тогда теоретические частоты вычисляются по формуле
Затем сравниваются наблюдаемое и критическое значение критерия Пирсона с учетом того, что число степеней свободы k = s – 2.
Пример . Для выборки, интервальный статистический ряд которой имеет вид
проверить при уровне значимости α = 0,05 гипотезу о.
Критерий Колмогорова.
На практике кроме критерия
часто
используется критерий Колмогорова, в
котором в качестве меры расхождения
между теоретическим и эмпирическим
распределениями рассматривают
максимальное значение абсолютной
величины разности между эмпирической
функцией распределения
и соответствующей теоретической функцией
распределения
, (1)
называемой статистикой критерия Колмогорова .
Доказано, что какова бы ни была функция
распределения
непрерывной случайной величины
,
при неограниченном увеличении числа
наблюдений
вероятность неравенства
стремится к пределу
Задавая уровень значимости
,
из соотношения
(3)
можно найти соответствующее критическое
значение
.
Схема применения критерия Колмогорова следующая:
. (4)
Замечание
Можно отметить, что решение подобных задач можно было бы найти с помощью критерия . Потенциальное преимущества критерия Колмогорова в том, что он не требует группирования данных (с неизбежной потерей информации), а дает возможность рассматривать индивидуальные наблюдаемые значения. Этот критерий можно успешно применять для малых выборок. Считается, что его мощность, вообще говоря, выше, чем у критерия .
Пример Получена
случайная выборка объема
.
Построим вариационный ряд и эмпирическую
функцию распределения:
|
|
|||||||
|
|
|||||||
|
|
Проверим гипотезу, что эти наблюдения
образуют случайную выборку из распределения
с уровнем значимости
.
Затем мы можем определить
графически либо аналитически, причем
эти значения должны появиться в точке
,
соответствующей одной из наблюдаемых
величин. С этой целью необходимо вычислить
пары величин
и
(см. рис. 1) для каждого значения выборки.
Для вычисления вспомним: , где - функция стандартного нормального распределения. Результаты всех вычислений представим в виде таблицы:
|
|
|
|
||
Из таблицы результатов следует:
.
Из статистических таблиц получим
.
Поскольку
,
то принимается гипотеза
,
т.е. можно считать, что данные подчиняются
распределению
.
Проверка гипотез об однородности выборок
Гипотезы об однородности выборок – это гипотезы о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности.
Пусть имеются две независимые выборки,
произведенные из генеральных совокупностей
с неизвестными теоретическими функциями
распределения
и
.
Проверяемая нулевая гипотеза имеет вид
против конкурирующей
.
Будем предполагать, что функции
и
непрерывны.
Критерий Колмогорова-Смирнова использует ту же самую идею, что и критерий Колмогорова, но только в критерии Колмогорова сравнивается эмпирическая функция распределения с теоретической, а в критерии Колмогорова-Смирнова сравниваются две эмпирические функции распределения.
Статистика критерия Колмогорова-Смирнова имеет вид:
,
где
и
– эмпирические функции распределения,
построенные по двум выборкам c
объемами
и
.
отвергается на уровне значимости
,
если фактически наблюдаемое значение
больше критического
,
т.е.
,
и принимается в противном случае.
Критерий Колмогорова-Смирнова в программе STATISTICA в среде Windows
Пример основан на исследовании агрессивности четырехлетних мальчиков и девочек (Siegel, S. (1956) Nonparametric statistics for the behavioral sciences (2nded.) New York: McGraw-Hill). Данные содержатся в файле Aggressn.sta.
Двенадцать мальчиков и двенадцать девочек наблюдались в течение 15-минутной игры; агрессивность каждого ребенка оценивалась в баллах (в терминах частоты и степени проявления агрессивности) и суммировалась в один индекс агрессивности, который вычислялся для каждого ребенка.
Задание анализа . Выберите Nonparametrics из меню Statistics. Затем выберете Comparing two independent samples (groups). Появится диалоговое окно Comparing Two Groups . Нажмите на кнопку Variables . Здесь выберете переменную variable Aggressn в Dependent variable list и переменную Gender в Indep . (grouping ) variable . Коды для однозначного отнесения каждого наблюдения к определенному полу будут автоматически выбраны программой.
Как видно из таблицы результатов, различие между агрессивностью мальчиков и девочек в этом исследовании высокозначимо.
На практике кроме критерия χ 2 часто используется критерий Колмогорова, в котором в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривают максимальное значение абсолютной величины разности между эмпирической функцией распределения и соответствующей теоретической функцией распределения
называемое статистикой критерия Колмогорова.
Задавая уровень значимости α, можно найти соответствующее критическое значение
В таблице приводятся критические значения , критерия Колмогорова для некоторых α.
Таблица 4.2.
Схема применения критерия Колмогорова
1.Строится эмпирическая функция распределения и предполагаемая теоретическая функция распределения F(x) .
2.Определяется статистика Колмогорова D – мера расхождения между теоретическим и эмпирическим распределением и вычисляется величина
3. Если вычисленное значение λ больше критического , то нулевая гипотеза Н 0 о том, что случайная величина Х имеет заданный закон распределения, отвергается.
Если , то считают, что гипотеза Н 0 не противоречит опытным данным.
Пример. С помощью критерия Колмогорова на уровне значимости α=0,05 проверить гипотезу Н 0 о том, что случайная величина Х – выработка рабочих предприятия – имеет нормальный закон распределения.
Решение . 1. Построим эмпирическую и теоретическую функции распределения.
Эмпирическую функцию распределения строят по относительным накопленным частотам.
Теоретическую функцию распределения построим согласно формуле
где
Результаты вычислений сведем в таблицу:
Таблица 4.3.
Критерий Колмогорова-Смирнова. Проверка гипотезы об однородности выборок
Гипотезы об однородности выборок – это гипотезы о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности.Пусть имеются две независимые выборки, произведенные из генеральных совокупностей с неизвестными теоретическими функциями распределения и .
Проверяемая нулевая гипотеза имеет вид против конкурирующей . Будем предполагать, что функции и непрерывны и для оценки используем статистику Колмогорова – Смирнова .
Критерий Колмогорова-Смирнова использует ту же самую идею, что и критерий Колмогорова. Однако различие заключается в том, что в критерии Колмогорова сравнивается эмпирическая функция распределения с теоретической, а в критерии Колмогорова-Смирнова сравниваются две эмпирические функции распределения.
Статистика критерия Колмогорова-Смирнова имеет вид:
, (9.1)
где и – эмпирические функции распределения, построенные по двум выборкам c объемами и .
Гипотеза отвергается, если фактически наблюдаемое значение статистики больше критического , т.е. , и принимается в противном случае.
При малых объемах выборок критические значения для заданных уровней значимости критерия можно найти в специальных таблицах. При (а практически при ) распределение статистики сводится к распределению Колмогорова для статистики . В этом случае гипотеза отвергается на уровне значимости , если фактически наблюдаемое значение больше критического , т.е. , и принимается в противном случае.
Пример 1. ^ ПРОВЕРКА ОДНОРОДНОСТИ ДВУХ ВЫБОРОК
Были осуществлены две проверки торговых точек с целью выявления недовесов. Полученные результаты сведены в таблицу:
| ^ Номер интервала | Интервалы недовесов, г | Частоты |
|
| Выборка 1 | Выборка 2 |
||
| 1 | 0 – 10 | 3 | 5 |
| 2 | 10 – 20 | 10 | 12 |
| 3 | 20 – 30 | 15 | 8 |
| 4 | 30 – 40 | 20 | 25 |
| 5 | 40 – 50 | 12 | 10 |
| 6 | 50 – 60 | 5 | 8 |
| 7 | 60 – 70 | 25 | 20 |
| 8 | 70 – 80 | 15 | 7 |
| 9 | 80 – 90 | 5 | 5 |
Объем первой выборки был равен , а второй – .
Решение :
Обозначим и – накопленные частоты выборок 1 и 2; 
, 
– значения их эмпирических функций распределения соответственно. Обработанные результаты сведем в таблицу:
| | | | | |  |
| 10 | 3 | 5 | 0.027 | 0.050 | 0.023 |
| 20 | 13 | 17 | 0.118 | 0.170 | 0.052 |
| 30 | 28 | 25 | 0.254 | 0.250 | 0.004 |
| 40 | 48 | 50 | 0.436 | 0.500 | 0.064 |
| 50 | 60 | 60 | 0.545 | 0.600 | 0.055 |
| 60 | 65 | 68 | 0.591 | 0.680 | 0.089 |
| 70 | 90 | 88 | 0.818 | 0.880 | 0.072 |
| 80 | 105 | 95 | 0.955 | 0.950 | 0.005 |
| 90 | 110 | 100 | 1.000 | 1.000 | 0.000 |
Из последнего столбца таблицы видно, что . По формуле (9.1) получим
. Из статистических таблиц известно, что . Так как , то принимается нулевая гипотеза , т.е. недовесы покупателям описываются одной и той же функцией распределения.^
СТАТИСТИЧЕСКАЯ НЕЗАВИСИМОСТЬ И ВЫЯВЛЕНИЕ ТРЕНДА
При анализе случайных данных часто возникает ситуации, когда требуется выяснить, являются ли наблюдения или оценки параметров статистически независимыми или же они подвержены тренду. Это особенно важно при анализе нестационарных данных.
Такие исследования, обычно, проводят на основе свободных от распределений
или непараметрических методов
, в которых относительно функции распределения исследуемых данных не делается никаких предположений.
^
Критерий серий
Рассмотрим последовательность наблюдённых значений случайной величины , причём каждое наблюдение отнесено к одному из двух взаимно исключаемых классов, которые можно обозначить просто (+) или
(–). Рассмотрим ряд примеров:
В каждом из этих примерах образуется последовательность вида:
^ Серией называется последовательность однотипных наблюдений, перед и после которой следуют наблюдения противоположного типа или же вообще нет никаких наблюдений.
В приведенной последовательности число наблюдений равно ; а количество серий равно .
Если последовательность наблюдений состоит из независимых исходов одной и той же случайной величины, т.е. если вероятность отдельных исходов [(+) или (−)] не меняется от наблюдения к наблюдению, то выборочное распределение числа серий в последовательности является случайной величиной со средним значением и дисперсией:
(9.2)
(9.3)
Здесь число исходов (+), а число исходов (−), естественно . В частном случае если , то:
. (9.4)
Предположим, что есть основание подозревать наличие тренда в последовательности наблюдений, т.е. есть основание считать, что вероятность появления (+) или (−) меняются от наблюдения к наблюдению. Существование тренда можно проверить следующим образом. Примем в качестве нулевой гипотезы тренда нет, т.е. предположим, что наблюдений являются независимыми исходами одной и той же случайной величины. Тогда для проверки гипотезы с любым требуемым уровнем значимости необходимо сравнить наблюденное число серий с границами области принятия гипотезы равными и , где .
Если наблюденное число серий окажется вне области принятия гипотезы, то нулевая гипотеза должна быть отвергнута с уровнем значимости . В противном случае нулевую гипотезу можно принять.
Пример 2. ^ ПРИМЕНЕНИЕ КРИТЕРИЯ СЕРИЙ
Имеется последовательность независимых наблюдений :
| 5.5 | 5.1 | 5.7 | 5.2 | 4.8 | 5.7 | 5.0 | 6.5 | 5.4 | 5.8 |
| 6.8 | 6.6 | 4.9 | 5.4 | 5.9 | 5.4 | 6.8 | 5.8 | 6.9 | 5.5 |
Проверим независимость наблюдений, подсчитав число серий в последовательности, полученной путем сравнения наблюдений с медианой. Применим критерий с уровнем значимости .
Из анализа данных получим, что значение является медианой. Тогда введем обозначения (+) при , (–) при . Итак, получим:
В нашем примере , а область принятия гипотезы имеет вид:
.
По статистическим таблицам находим . Т.к.
