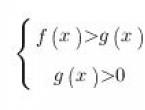Cum se rezolvă inegalitățile logaritmice simple. Rezolvarea inegalităților logaritmice simple
Inegalități logaritmice
În lecțiile anterioare, ne-am familiarizat cu ecuațiile logaritmice și acum știm ce sunt acestea și cum să le rezolvăm. Lecția de astăzi va fi dedicată studiului inegalităților logaritmice. Care sunt aceste inegalități și care este diferența dintre rezolvarea unei ecuații logaritmice și a unei inegalități?
Inegalitățile logaritmice sunt inegalități care au o variabilă care apare sub semnul logaritmului sau la baza acestuia.
Sau, mai putem spune că o inegalitate logaritmică este o inegalitate în care valoarea ei necunoscută, ca într-o ecuație logaritmică, va apărea sub semnul logaritmului.
Cele mai simple inegalități logaritmice au următoarea formă:
unde f(x) și g(x) sunt niște expresii care depind de x.
Să ne uităm la asta folosind acest exemplu: f(x)=1+2x+x2, g(x)=3x−1.
Rezolvarea inegalităților logaritmice
Înainte de a rezolva inegalitățile logaritmice, este de remarcat faptul că, atunci când sunt rezolvate, acestea sunt similare cu inegalitățile exponențiale, și anume:
În primul rând, când trecem de la logaritmi la expresii sub semnul logaritmului, trebuie să comparăm și baza logaritmului cu una;
În al doilea rând, atunci când rezolvăm o inegalitate logaritmică folosind o modificare a variabilelor, trebuie să rezolvăm inegalitățile în raport cu modificarea până când obținem cea mai simplă inegalitate.
Dar tu și cu mine am luat în considerare aspecte similare ale rezolvării inegalităților logaritmice. Acum să acordăm atenție unei diferențe destul de semnificative. Tu și cu mine știm că funcția logaritmică are un domeniu limitat de definiție, prin urmare, atunci când trecem de la logaritmi la expresii sub semnul logaritmului, trebuie să luăm în considerare intervalul de valori admisibile (ADV).
Adică, trebuie luat în considerare faptul că atunci când rezolvăm o ecuație logaritmică, tu și cu mine putem găsi mai întâi rădăcinile ecuației și apoi verificăm această soluție. Dar rezolvarea unei inegalități logaritmice nu va funcționa în acest fel, deoarece trecând de la logaritmi la expresii sub semnul logaritmului, va fi necesar să se noteze ODZ a inegalității.
În plus, merită să ne amintim că teoria inegalităților constă din numere reale, care sunt numere pozitive și negative, precum și din numărul 0.
De exemplu, când numărul „a” este pozitiv, atunci trebuie să utilizați următoarea notație: a >0. În acest caz, atât suma, cât și produsul acestor numere vor fi, de asemenea, pozitive.
Principiul principal pentru rezolvarea unei inegalități este înlocuirea acesteia cu o inegalitate mai simplă, dar principalul lucru este că este echivalentă cu cea dată. În plus, am obținut și o inegalitate și am înlocuit-o din nou cu una care are o formă mai simplă etc.
Când rezolvați inegalitățile cu o variabilă, trebuie să găsiți toate soluțiile acesteia. Dacă două inegalități au aceeași variabilă x, atunci astfel de inegalități sunt echivalente, cu condiția ca soluțiile lor să coincidă.
Când efectuați sarcini de rezolvare a inegalităților logaritmice, trebuie să vă amintiți că atunci când a > 1, atunci funcția logaritmică crește și când 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Metode de rezolvare a inegalităților logaritmice
Acum să ne uităm la câteva dintre metodele care au loc atunci când se rezolvă inegalitățile logaritmice. Pentru o mai bună înțelegere și asimilare, vom încerca să le înțelegem folosind exemple specifice.
Știm cu toții că cea mai simplă inegalitate logaritmică are următoarea formă:
În această inegalitate, V – este unul dintre următoarele semne de inegalitate:<,>, ≤ sau ≥.
Când baza unui logaritm dat este mai mare decât unu (a>1), făcând tranziția de la logaritmi la expresii sub semnul logaritmului, atunci în această versiune semnul de inegalitate este păstrat, iar inegalitatea va avea următoarea formă:
care este echivalent cu acest sistem:

În cazul în care baza logaritmului este mai mare decât zero și mai mică decât unu (0 Acesta este echivalent cu acest sistem: Să ne uităm la mai multe exemple de rezolvare a celor mai simple inegalități logaritmice prezentate în imaginea de mai jos: Exercițiu. Să încercăm să rezolvăm această inegalitate: Rezolvarea intervalului de valori acceptabile. Acum să încercăm să-i înmulțim partea dreaptă cu: Să vedem cu ce putem veni: Acum, să trecem la conversia expresiilor sublogaritmice. Datorită faptului că baza logaritmului este 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x - 8 > 16; Și de aici rezultă că intervalul pe care l-am obținut aparține în întregime ODZ și este o soluție la o astfel de inegalitate. Iată răspunsul pe care l-am primit: Acum să încercăm să analizăm de ce avem nevoie pentru a rezolva cu succes inegalitățile logaritmice? În primul rând, concentrează-ți toată atenția și încearcă să nu faci greșeli atunci când faci transformările care sunt date în această inegalitate. De asemenea, trebuie amintit că atunci când se rezolvă astfel de inegalități, este necesar să se evite extinderile și contracțiile inegalităților, care pot duce la pierderea sau achiziționarea de soluții străine. În al doilea rând, atunci când rezolvați inegalități logaritmice, trebuie să învățați să gândiți logic și să înțelegeți diferența dintre concepte precum un sistem de inegalități și un set de inegalități, astfel încât să puteți selecta cu ușurință soluții la inegalitate, ghidându-vă în același timp de DL-ul său. În al treilea rând, pentru a rezolva cu succes astfel de inegalități, fiecare dintre voi trebuie să cunoască perfect toate proprietățile funcțiilor elementare și să înțeleagă clar sensul acestora. Astfel de funcții includ nu numai logaritmice, ci și raționale, de putere, trigonometrice etc., într-un cuvânt, toate cele pe care le-ați studiat în timpul algebrei școlare. După cum puteți vedea, după ce ați studiat subiectul inegalităților logaritmice, nu este nimic dificil în rezolvarea acestor inegalități, cu condiția să fiți atent și perseverent în atingerea obiectivelor. Pentru a evita orice probleme în rezolvarea inegalităților, trebuie să exersați cât mai mult posibil, rezolvând diverse sarcini și, în același timp, să vă amintiți metodele de bază de rezolvare a unor astfel de inegalități și sistemele lor. Dacă nu reușiți să rezolvați inegalitățile logaritmice, ar trebui să vă analizați cu atenție greșelile pentru a nu mai reveni la ele în viitor. Pentru a înțelege mai bine subiectul și a consolida materialul tratat, rezolvați următoarele inegalități: O inegalitate se numește logaritmică dacă conține o funcție logaritmică. Metodele de rezolvare a inegalităților logaritmice nu sunt diferite de, cu excepția a două lucruri. În primul rând, când se trece de la inegalitatea logaritmică la inegalitatea funcțiilor sublogaritmice, ar trebui urmați semnul inegalității rezultate. Se supune următoarei reguli. Dacă baza funcției logaritmice este mai mare de $1$, atunci când treceți de la inegalitatea logaritmică la inegalitatea funcțiilor sublogaritmice, semnul inegalității se păstrează, dar dacă este mai mic de $1$, atunci se schimbă la opus . În al doilea rând, soluția oricărei inegalități este un interval și, prin urmare, la sfârșitul rezolvării inegalității funcțiilor sublogaritmice este necesar să se creeze un sistem de două inegalități: prima inegalitate a acestui sistem va fi inegalitatea funcțiilor sublogaritmice, iar al doilea va fi intervalul domeniului de definire a funcţiilor logaritmice incluse în inegalitatea logaritmică. Să rezolvăm inegalitățile: 1.
$\log_(2)((x+3)) \geq 3.$ $D(y): \x+3>0.$ $x \in (-3;+\infty)$ Baza logaritmului este $2>1$, deci semnul nu se schimbă. Folosind definiția logaritmului, obținem: $x+3 \geq 2^(3),$ $x \in )


Rezolvarea exemplelor
![]()



3x > 24;
x > 8. ![]()
Ce este necesar pentru a rezolva inegalitățile logaritmice?
Teme pentru acasă

Practică.